orx-marching-squares

Tools for extracting contours from functions

How to use it?

orx-marching-squares provides the findContours() function

fun f(v: Vector2) = v.distanceTo(drawer.bounds.center) - 200.0
val contours = findContours(::f, drawer.bounds, 16.0)
drawer.contours(contours)

With a small adjustment to the given function one can use findContours to find iso contours. The trick is to add a cosine over the distance function.

fun f(v: Vector2) = cos((v.distanceTo(drawer.bounds.center) / 100.0) * 2 * PI)
val contours = findContours(::f, drawer.bounds.offsetEdges(32.0), 16.0)
drawer.contours(contours)

Demos

FindContours01

A simple demonstration of using the findContours method provided by orx-marching-squares.

findContours lets one generate contours by providing a mathematical function to be sampled within the provided area and with the given cell size. Contours are generated between the areas in which the function returns positive and negative values.

In this example, the f function returns the distance of a point to the center of the window minus 200.0. Therefore, sampled locations which are less than 200 pixels away from the center return negative values and all others return positive values, effectively generating a circle of radius 200.0.

Try increasing the cell size to see how the precision of the circle reduces.

The circular contour created in this program has over 90 segments. The number of segments depends on the cell size, and the resulting radius.

source code

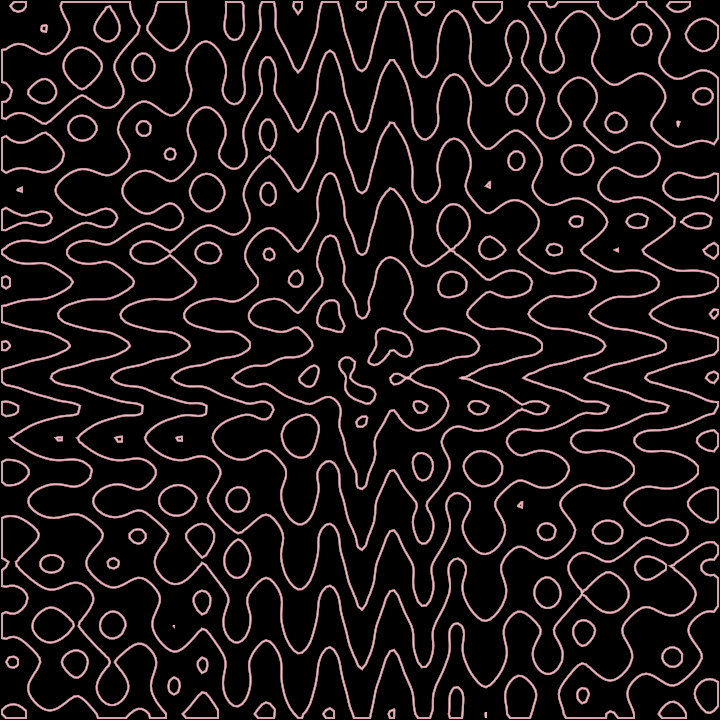
FindContours02

This Marching Square demonstration shows the effect of wrapping a distance function within a cosine (or sine). These mathematical functions return values that periodically alternate between negative and positive, creating nested contours as the distance increases.

The / 100.0) * 2 * PI part of the formula is only a scaling factor, more or less equivalent to 0.06. Increasing or decreasing this value will change how close the generated parallel curves are to each other.

source code

FindContours03

Demonstrates how Marching Squares can be used to generate animations, by using a time-related variable like seconds. The evaluated function is somewhat more complex than previous ones, but one can arrive to such functions by exploration and experimentation, nesting trigonometrical functions and making use of seconds, v.x and v.y.

source code

FindContours04

Demonstrates using Marching Squares while reading the pixel colors of a loaded image.

Notice how the area defined when calling findContours is larger than the window.

Using point coordinates from such an area to read from image pixels might cause problems when points are outside the image bounds, therefore the f function checks whether the requested v is within bounds, and only reads from the image when it is.

The seconds built-in variable is used to generate an animated effect, serving as a shifting cut-off point that specifies at which brightness level to create curves.

source code