add demos to README.md

orx-marching-squares/README.md

@@ -23,7 +23,20 @@ drawer.contours(contours)
 ## Demos
 ### FindContours01
 
+A simple demonstration of using the `findContours` method provided by `orx-marching-squares`.
 
+`findContours` lets one generate contours by providing a mathematical function to be
+sampled within the provided area and with the given cell size. Contours are generated
+between the areas in which the function returns positive and negative values.
+
+In this example, the `f` function returns the distance of a point to the center of the window minus 200.0.
+Therefore, sampled locations which are less than 200 pixels away from the center return
+negative values and all others return positive values, effectively generating a circle of radius 200.0.
+
+Try increasing the cell size to see how the precision of the circle reduces.
+
+The circular contour created in this program has over 90 segments. The number of segments depends on the cell
+size, and the resulting radius.
 
 ![FindContours01Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-marching-squares/images/FindContours01Kt.png)
 
@@ -31,6 +44,13 @@ drawer.contours(contours)
 
 ### FindContours02
 
+This Marching Square demonstration shows the effect of wrapping a distance function
+within a cosine (or sine). These mathematical functions return values that periodically
+alternate between negative and positive, creating nested contours as the distance increases.
+
+The `/ 100.0) * 2 * PI` part of the formula is only a scaling factor, more or less
+equivalent to 0.06. Increasing or decreasing this value will change how close the generated
+parallel curves are to each other.
 
 
 ![FindContours02Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-marching-squares/images/FindContours02Kt.png)
@@ -39,6 +59,10 @@ drawer.contours(contours)
 
 ### FindContours03
 
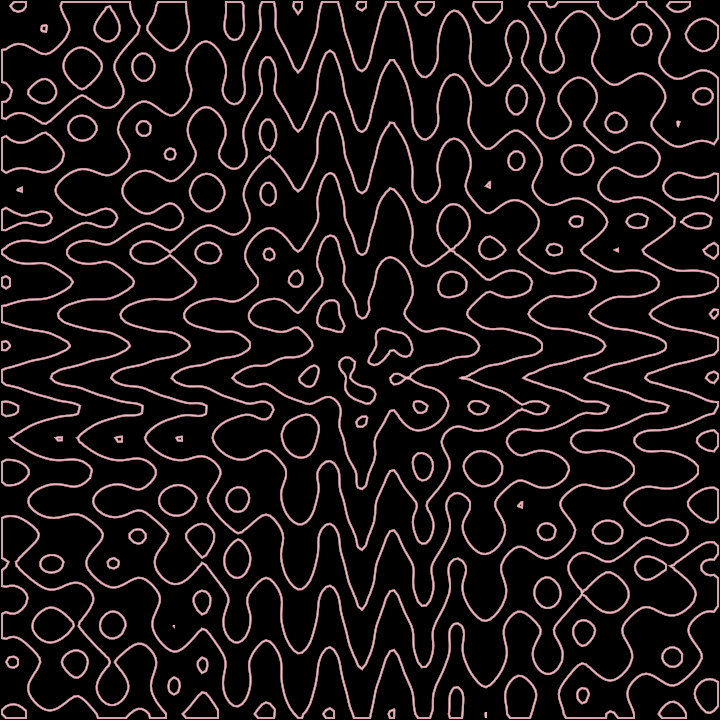
+Demonstrates how Marching Squares can be used to generate animations, by using a time-related
+variable like `seconds`. The evaluated function is somewhat more complex than previous ones,
+but one can arrive to such functions by exploration and experimentation, nesting trigonometrical
+functions and making use of `seconds`, v.x and v.y.
 
 
 ![FindContours03Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-marching-squares/images/FindContours03Kt.png)
@@ -47,7 +71,16 @@ drawer.contours(contours)
 
 ### FindContours04
 
+Demonstrates using Marching Squares while reading the pixel colors of a loaded image.
 
+Notice how the area defined when calling `findContours` is larger than the window.
+
+Using point coordinates from such an area to read from image pixels might cause problems when points are
+outside the image bounds, therefore the `f` function checks whether the requested `v` is within bounds,
+and only reads from the image when it is.
+
+The `seconds` built-in variable is used to generate an animated effect, serving as a shifting cut-off point
+that specifies at which brightness level to create curves.
 
 ![FindContours04Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-marching-squares/images/FindContours04Kt.png)
 

orx-math/README.md

@@ -8,6 +8,24 @@ linear ranges, simplex ranges, matrices and radial basis functions (RBF).
 ## Demos
 ### linearrange/DemoLinearRange02
 
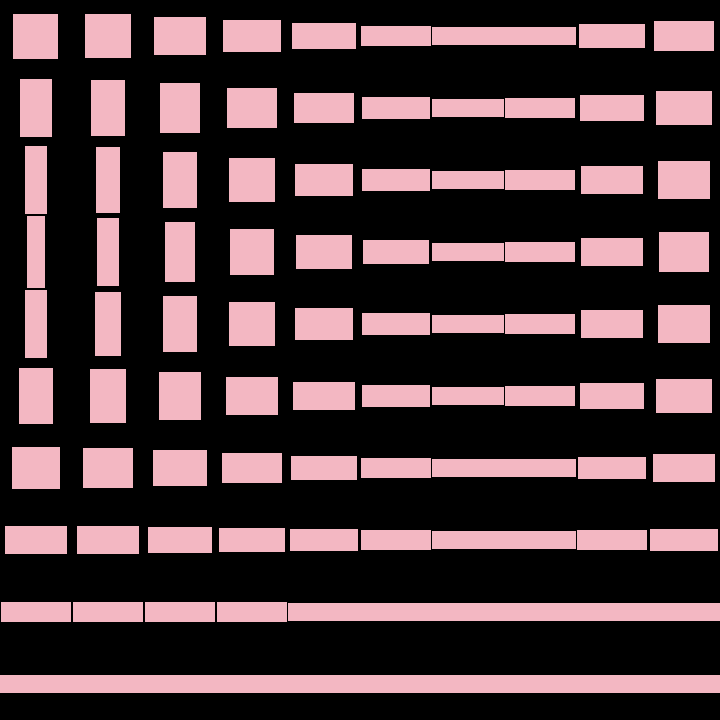
+Demonstrate how to create a 1D linear range between two instances of a `LinearType`, in this case,
+a horizontal `Rectangle` and a vertical one.
+
+Notice how the `..` operator is used to construct the `LinearRange1D`.
+
+The resulting `LinearRange1D` provides a `value()` method that takes a normalized
+input and returns an interpolated value between the two input elements.
+
+This example draws a grid of rectangles interpolated between the horizontal and the vertical
+triangles. The x and y coordinates and the `seconds` variable are used to specify the
+interpolation value for each grid cell.
+
+One can use the `LinearRange` class to construct
+- a `LinearRange2D` out of two `LinearRange1D`
+- a `LinearRange3D` out of two `LinearRange2D`
+- a `LinearRange4D` out of two `LinearRange3D`
+
+(not demonstrated here)
 
 
 ![linearrange-DemoLinearRange02Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-math/images/linearrange-DemoLinearRange02Kt.png)
@@ -16,6 +34,13 @@ linear ranges, simplex ranges, matrices and radial basis functions (RBF).
 
 ### linearrange/DemoLinearRange03
 
+Demonstrates how to create a `LinearRange2D` out of two `LinearRange1D` instances.
+The first range interpolates a horizontal rectangle into a vertical one.
+The second range interpolates two smaller squares of equal size, one placed
+higher along the y-axis and another one lower.
+
+A grid of such rectangles is displayed, animating the `u` and `v` parameters based on
+`seconds`, `x` and `y` indices. The second range results in a vertical wave effect.
 
 
 ![linearrange-DemoLinearRange03Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-math/images/linearrange-DemoLinearRange03Kt.png)
@@ -24,12 +49,12 @@ linear ranges, simplex ranges, matrices and radial basis functions (RBF).
 
 ### matrix/DemoLeastSquares01
 
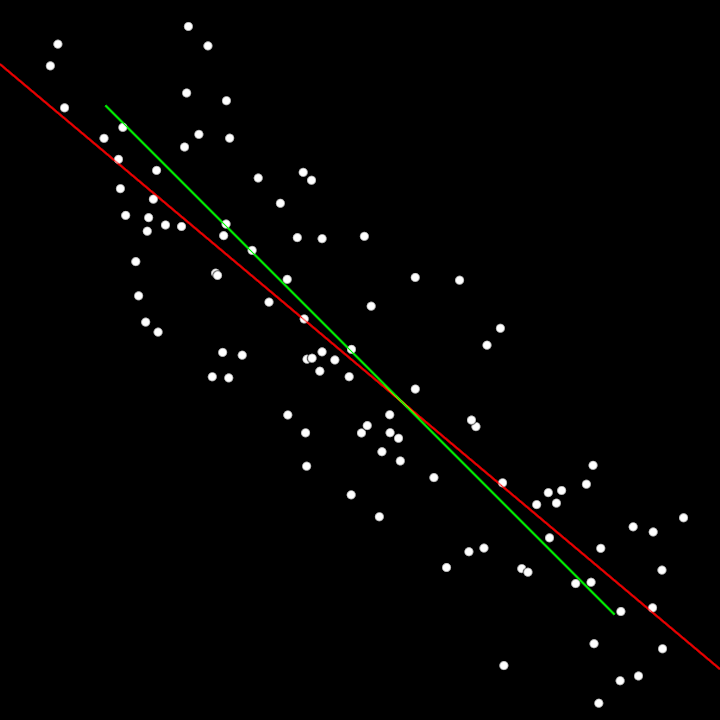
-Demonstrate least squares method to find a regression line through noisy points
+Demonstrate least squares method to find a regression line through noisy points.
-Line drawn in red is the estimated line, in green is the ground-truth line
+The line drawn in red is the estimated line. The green one is the ground-truth.
 
-Ax = b => x = A⁻¹b
+`Ax = b => x = A⁻¹b`
-because A is likely inconsistent, we look for an approximate x based on AᵀA, which is consistent.
+because `A` is likely inconsistent, we look for an approximate `x` based on `AᵀA`, which is consistent.
-x̂ = (AᵀA)⁻¹ Aᵀb
+`x̂ = (AᵀA)⁻¹ Aᵀb`
 
 ![matrix-DemoLeastSquares01Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-math/images/matrix-DemoLeastSquares01Kt.png)
 
@@ -37,7 +62,17 @@ x̂ = (AᵀA)⁻¹ Aᵀb
 
 ### matrix/DemoLeastSquares02
 
-Demonstrate least squares method to fit a cubic bezier to noisy points
+Demonstrate how to use the `least squares` method to fit a cubic bezier to noisy points.
+
+On every animation frame, 10 concentric circles are created centered on the window and converted to contours.
+In OPENRNDR, circular contours are made ouf of 4 cubic-Bezier curves. Each of those curves is considered
+one by one as the ground truth, then 5 points are sampled near those curves.
+Finally, two matrices are constructed using those points and math operations are applied to
+revert the randomization attempting to reconstruct the original curves.
+
+The result is drawn on every animation frame, revealing concentric circles that are more or less similar
+to the ground truth depending on the random values used.
+
 
 ![matrix-DemoLeastSquares02Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-math/images/matrix-DemoLeastSquares02Kt.png)
 
@@ -45,7 +80,27 @@ Demonstrate least squares method to fit a cubic bezier to noisy points
 
 ### rbf/RbfInterpolation01
 
+Demonstrates using a two-dimensional Radial Basis Function (RBF) interpolator
+with the user provided 2D input points, their corresponding values (colors in this demo),
+a smoothing factor, and a radial basis function kernel.
 
+The program chooses 14 random points in the window area leaving a 100 pixels
+margin around the borders and assigns a randomized color to each point.
+
+Next it creates the interpolator using those points and colors, a smoothing factor
+and the RBF function used for interpolation. This function takes a squared distance
+as input and returns a scalar value representing the influence of points at that distance.
+
+A ShadeStyle implementing the RBF interpolation is created next, used to render
+the background gradient interpolating all points and their colors.
+
+After rendering the background, the original points and their colors are
+drawn as circles for reference.
+
+Finally, the current mouse position is used for sampling a color
+from the interpolator and displayed for comparison. Notice that even if
+the fill color is flat, it may look like a gradient due to the changing
+colors in the surrounding pixels.
 
 ![rbf-RbfInterpolation01Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-math/images/rbf-RbfInterpolation01Kt.png)
 
@@ -53,7 +108,27 @@ Demonstrate least squares method to fit a cubic bezier to noisy points
 
 ### rbf/RbfInterpolation02
 
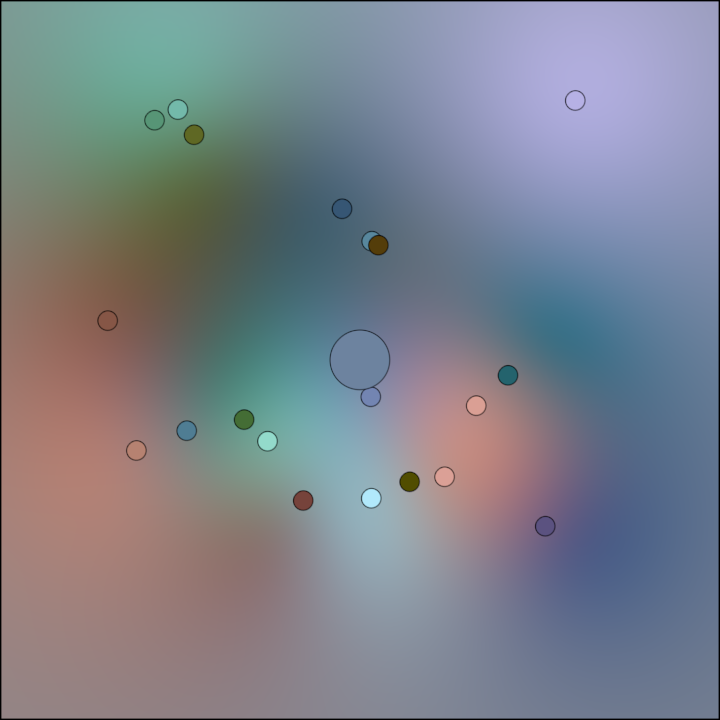
+Demonstrates using a two-dimensional Radial Basis Function (RBF) interpolator
+with the user provided 2D input points, their corresponding values (colors in this demo),
+a smoothing factor, and a radial basis function kernel.
 
+The program chooses 20 random points in the window area leaving a 100 pixels
+margin around the borders and assigns a randomized color to each point.
+
+Next it creates the interpolator using those points and colors, a smoothing factor
+and the RBF function used for interpolation. This function takes a squared distance
+as input and returns a scalar value representing the influence of points at that distance.
+
+A ShadeStyle implementing the same RBF interpolation is created next, used to render
+the background gradient interpolating all points and their colors.
+
+After rendering the background, the original points and their colors are
+drawn as circles for reference.
+
+Finally, the current mouse position is used for sampling a color
+from the interpolator and displayed for comparison. Notice that even if
+the fill color is flat, it may look like a gradient due to the changing
+colors in the surrounding pixels.
 
 ![rbf-RbfInterpolation02Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-math/images/rbf-RbfInterpolation02Kt.png)
 
@@ -61,7 +136,17 @@ Demonstrate least squares method to fit a cubic bezier to noisy points
 
 ### simplexrange/DemoSimplexRange3D01
 
+Demonstrates the use of the `SimplexRange3D` class. Its constructor takes 4 instances of a `LinearType`
+(something that can be interpolated linearly, like `ColorRGBa`). The `SimplexRange3D` instance provides
+a `value()` method that returns a `LinearType` interpolated across the 4 constructor arguments using
+a normalized 3D coordinate.
 
+This demo program creates a 3D grid of 20x20x20 unit 3D cubes. Their color is set by interpolating
+their XYZ index across the 4 input colors.
+
+2D, 4D and ND varieties are also provided by `SimplexRange`.
+
+Simplex Range* is not to be confused with *Simplex Noise*.
 
 ![simplexrange-DemoSimplexRange3D01Kt](https://raw.githubusercontent.com/openrndr/orx/media/orx-math/images/simplexrange-DemoSimplexRange3D01Kt.png)