add demos to README.md
This commit is contained in:
@@ -189,7 +189,9 @@ val v8 = billow(seed, x, y, z, ::perlinLinear, octaves, lacunarity, gain)
|
||||
## Demos
|
||||
### DemoCubicNoise2D01
|
||||
|
||||
|
||||
Demonstrates how to render dynamic grayscale patterns using 3D cubic Hermite interpolation.
|
||||
The program draws one point per pixel on the screen, calculating the color intensity of each point
|
||||
based on a 3D cubic Hermite noise function.
|
||||
|
||||

|
||||
|
||||
@@ -197,7 +199,12 @@ val v8 = billow(seed, x, y, z, ::perlinLinear, octaves, lacunarity, gain)
|
||||
|
||||
### DemoFunctionalComposition01
|
||||
|
||||
Demonstrates how to chain methods behind noise functions like `simplex3D` to
|
||||
alter its output. By default `simplex3D` produces one double value, but
|
||||
by calling `.withVector2Output()` it produces `Vector2` instances instead.
|
||||
|
||||
The `.gradient()` method alters the output to return the direction of fastest
|
||||
increase. Read more in [WikiPedia](https://en.wikipedia.org/wiki/Gradient).
|
||||
|
||||

|
||||
|
||||
@@ -205,7 +212,15 @@ val v8 = billow(seed, x, y, z, ::perlinLinear, octaves, lacunarity, gain)
|
||||
|
||||
### DemoGradientPerturb2D
|
||||
|
||||
Demonstrates how to generate a dynamic fractal-based visual effect
|
||||
using 2D gradient perturbation and simplex noise.
|
||||
|
||||
This method initializes a color buffer to create an image and applies fractal gradient noise to set
|
||||
each pixel's brightness, producing a dynamic visual texture. The fractal effect is achieved by layering multiple
|
||||
levels of noise, and each pixel's color intensity is based on the noise function results.
|
||||
The output is continuously updated to produce animated patterns.
|
||||
|
||||
CPU-based.
|
||||
|
||||

|
||||
|
||||
@@ -213,7 +228,15 @@ val v8 = billow(seed, x, y, z, ::perlinLinear, octaves, lacunarity, gain)
|
||||
|
||||
### DemoGradientPerturb3D
|
||||
|
||||
Demonstrates how to generate a dynamically evolving visual
|
||||
representation of fractal noise. The program uses 3D gradient perturbation and simplex noise
|
||||
to produce a grayscale gradient on a color buffer.
|
||||
|
||||
The visual output is created by iteratively computing the fractal gradient perturbation and simplex
|
||||
noise for each pixel in the color buffer, applying a perturbation based on time, and rendering the
|
||||
result as an image.
|
||||
|
||||
CPU-based.
|
||||
|
||||

|
||||
|
||||
@@ -221,7 +244,15 @@ val v8 = billow(seed, x, y, z, ::perlinLinear, octaves, lacunarity, gain)
|
||||
|
||||
### DemoScatter01
|
||||
|
||||
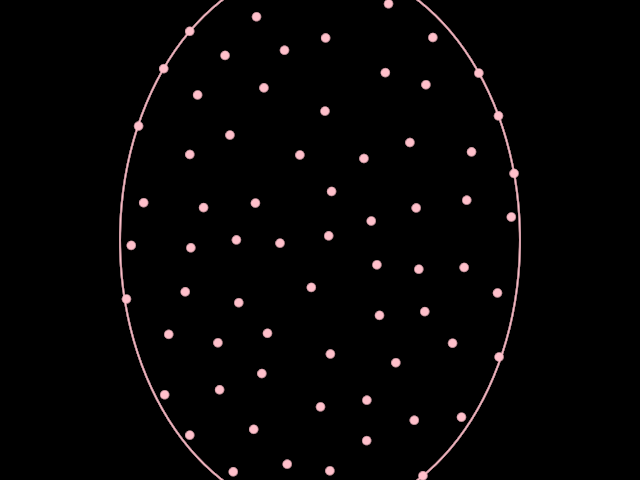
Demonstrates how to create an animated visualization of scattered points.
|
||||
|
||||
The program creates an animated ellipse with increasing and decreasing height.
|
||||
Then, scatters points inside it with a placementRadius of 20.0.
|
||||
|
||||
The animation reveals that the scattering positions are somewhat stable between
|
||||
animation frames.
|
||||
|
||||
The ellipse's contour is revealed and hidden every other second.
|
||||
|
||||
|
||||
|
||||
@@ -229,7 +260,12 @@ val v8 = billow(seed, x, y, z, ::perlinLinear, octaves, lacunarity, gain)
|
||||
|
||||
### DemoSimplex01
|
||||
|
||||
Demonstrates how to use the `simplex` method to obtain noise values based on a seed and an x value.
|
||||
|
||||
The program creates 20 horizontal contours with 40 steps each in which each 2D step and each 2D control point
|
||||
is affected by noise.
|
||||
|
||||
Time is used as a noise argument to produce an animated effect.
|
||||
|
||||

|
||||
|
||||
@@ -246,7 +282,11 @@ Demonstrate the generation of uniformly distributed points inside a list of tria
|
||||
|
||||
### DemoValueNoise2D01
|
||||
|
||||
Demonstrates how to render grayscale noise patterns dynamically using 3D quintic noise.
|
||||
|
||||
The program draws one point per pixel on the screen, calculating the color intensity of
|
||||
each point based on a 3D quintic noise function. The noise value is influenced by the
|
||||
pixel's 2D coordinates and animated over time.
|
||||
|
||||

|
||||
|
||||
@@ -275,7 +315,10 @@ The noise color can be set using a `color` or a `gain` property.
|
||||
|
||||
### glsl/DemoSimplexGLSL
|
||||
|
||||
A sine oscillator with randomized parameters
|
||||
Render an animated Simplex3D texture using shaders.
|
||||
|
||||
The uniforms in the shader are controlled by
|
||||
randomized sine oscillators.
|
||||
|
||||

|
||||
|
||||
@@ -285,8 +328,7 @@ A sine oscillator with randomized parameters
|
||||
|
||||
Demo that visualizes a 2D Hammersley point set.
|
||||
|
||||
The application is configured to run at 720x720 resolution. The program computes
|
||||
400 2D Hammersley points mapped within the bounds of the application's resolution.
|
||||
The program computes 400 2D Hammersley points mapped within the window bounds.
|
||||
These points are visualized by rendering circles at their respective positions.
|
||||
|
||||

|
||||
@@ -297,14 +339,12 @@ These points are visualized by rendering circles at their respective positions.
|
||||
|
||||
Demo program rendering a 3D visualization of points distributed using the Hammersley sequence in 3D space.
|
||||
|
||||
The application is set up at a resolution of 720x720 pixels. Within the visual
|
||||
program, a sphere mesh is created and a set of 1400 points is generated using
|
||||
the Hammersley sequence. Each point is translated and rendered as a small sphere
|
||||
in 3D space. This is achieved by mapping the generated points into a scaled domain.
|
||||
A set of 1400 points is generated using the Hammersley sequence.
|
||||
Each point is translated and rendered as a small sphere
|
||||
in 3D space.
|
||||
|
||||
The rendering utilizes the Orbital extension, enabling an interactive 3D camera
|
||||
to navigate the scene. The visualization relies on the draw loop for continuous
|
||||
rendering of the points.
|
||||
The rendering uses the Orbital extension, enabling an interactive 3D camera
|
||||
to navigate the scene.
|
||||
|
||||

|
||||
|
||||
@@ -312,17 +352,15 @@ rendering of the points.
|
||||
|
||||
### hammersley/DemoHammersley4D01
|
||||
|
||||
Demo that visualizes a 4D Hammersley point set in a 3D space, with colors determined by the 4th dimension.
|
||||
Demo visualizing a 4D Hammersley point set in a 3D space, with colors determined by the 4th dimension.
|
||||
|
||||
The application is configured at a resolution of 720x720 pixels. A sphere mesh is created
|
||||
using the `sphereMesh` utility, and a total of 10,000 4D points are generated with the
|
||||
`hammersley4D` sequence. These points are scaled, translated, and rendered as small spheres.
|
||||
A total of 10,000 4D points are generated with the `hammersley4D` sequence.
|
||||
These points are mapped to a cubical volume and rendered as small spheres.
|
||||
The color of each sphere is modified based on the 4th dimension of its corresponding point by
|
||||
shifting the hue in HSV color space.
|
||||
|
||||
This program employs the `Orbital` extension, enabling camera interaction for 3D navigation
|
||||
of the scene. Rendering occurs within the draw loop, providing continuous visualization
|
||||
of the point distribution.
|
||||
of the scene.
|
||||
|
||||
|
||||
|
||||
@@ -330,7 +368,15 @@ of the point distribution.
|
||||
|
||||
### hash/DemoCircleHash01
|
||||
|
||||
Demonstrates how to draw circles distributed within two subregions of a rectangular area
|
||||
using uniform random distribution and a hash-based method for randomness.
|
||||
|
||||
The application divides the window area into two subregions, offsets the edges inwards,
|
||||
and then calculates two circles representing these subregions. Points are then generated and drawn
|
||||
within these circles using two different methods:
|
||||
|
||||
- A uniform random distribution within the first circle.
|
||||
- A hash-based deterministic random point generation within the second circle.
|
||||
|
||||

|
||||
|
||||
@@ -338,7 +384,12 @@ of the point distribution.
|
||||
|
||||
### hash/DemoRectangleHash01
|
||||
|
||||
Demonstrates how to generate and draw random points within two subregions of a rectangular area
|
||||
using two different randomization methods.
|
||||
|
||||
The first subregion generates points using a _uniform_ random distribution, while the second subregion
|
||||
generates points deterministically with a _hash-based_ randomization approach. The points are visualized
|
||||
as small circles.
|
||||
|
||||

|
||||
|
||||
@@ -346,7 +397,12 @@ of the point distribution.
|
||||
|
||||
### hash/DemoUHash01
|
||||
|
||||
Demonstrates how to render a dynamic grid of points where the color of each point
|
||||
is determined using a hash-based noise generation method.
|
||||
|
||||
The application dynamically updates the visual output by calculating a 3D hash
|
||||
value for each point in the grid, based on the current time and the point's coordinates.
|
||||
The hash value is then used to determine the grayscale color intensity of each point.
|
||||
|
||||

|
||||
|
||||
@@ -354,15 +410,36 @@ of the point distribution.
|
||||
|
||||
### linearrange/DemoLinearRange01
|
||||
|
||||
Demonstrates how to create a linear range with two [org.openrndr.shape.Rectangle]s.
|
||||
|
||||
This range is then sampled at 100 random locations using the `uniform` method to get and render interpolated
|
||||
rectangles. The random seed changes once per second.
|
||||
|
||||
|
||||
|
||||
[source code](src/jvmDemo/kotlin/linearrange/DemoLinearRange01.kt)
|
||||
|
||||
### linearrange/DemoLinearRange02
|
||||
|
||||
Demonstrates how to create a linear range with two [org.openrndr.shape.Circle]s.
|
||||
|
||||
This range is then sampled at 100 random locations using the `hash` method to get and render interpolated
|
||||
circles. The random seed changes once per second.
|
||||
|
||||
Colors are calculated based on the index of each circle.
|
||||
|
||||

|
||||
|
||||
[source code](src/jvmDemo/kotlin/linearrange/DemoLinearRange02.kt)
|
||||
|
||||
### phrases/DemoUHashPhrase01
|
||||
|
||||
Demonstrate uniform hashing function phrase in a shadestyle
|
||||
Demonstrate the use of a uniform hashing function phrase in a ShadeStyle.
|
||||
|
||||
The hashing function uses the screen coordinates and the current time to
|
||||
calculate the brightness of each pixel.
|
||||
|
||||
Multiple GLSL hashing functions are defined in orx-shader-phrases.
|
||||
|
||||

|
||||
|
||||
@@ -370,8 +447,7 @@ Demonstrate uniform hashing function phrase in a shadestyle
|
||||
|
||||
### rseq/DemoRseq2D01
|
||||
|
||||
This demo sets up a window with dimensions 720x720 and renders frames
|
||||
demonstrating 2D quasirandomly distributed points. The points are generated
|
||||
Demonstrates quasirandomly distributed 2D points. The points are generated
|
||||
using the R2 sequence and drawn as circles with a radius of 5.0.
|
||||
|
||||

|
||||
@@ -380,7 +456,7 @@ using the R2 sequence and drawn as circles with a radius of 5.0.
|
||||
|
||||
### rseq/DemoRseq3D01
|
||||
|
||||
This demo renders a 3D visualizationof points distributed using the R3 quasirandom sequence. Each point is
|
||||
This demo renders a 3D visualization of points distributed using the R3 quasirandom sequence. Each point is
|
||||
represented as a sphere and positioned in 3D space based on the quasirandom sequence values.
|
||||
|
||||
The visualization setup includes:
|
||||
|
||||
@@ -172,13 +172,35 @@ The core elements to study to in this demo are `adjustContourSequence` and `laun
|
||||
|
||||
[source code](src/jvmDemo/kotlin/adjust/DemoAdjustContourContinue01.kt)
|
||||
|
||||
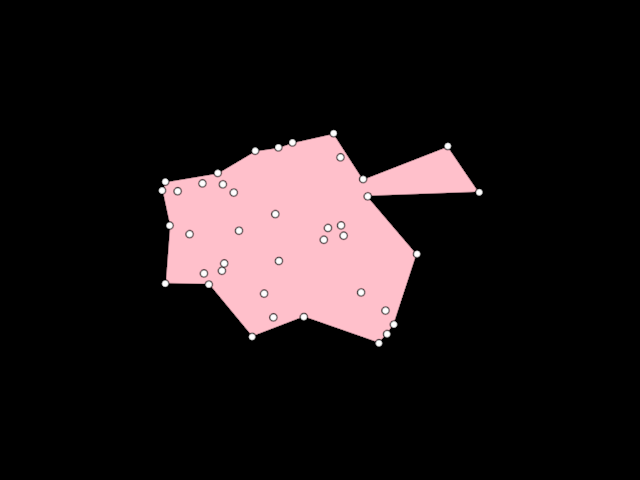
### alphashape/DemoAlphaShape
|
||||
### alphashape/DemoAlphaShape01
|
||||
|
||||
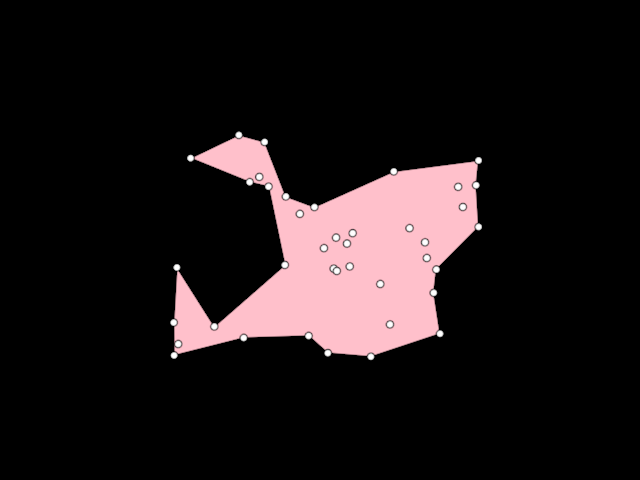
Demonstrates the use of [AlphaShape] to create a [org.openrndr.shape.ShapeContour] out
|
||||
of a collection of random [Vector2] points. Unlike the convex hull, an Alpha shape can be concave.
|
||||
|
||||
More details in [WikiPedia](https://en.wikipedia.org/wiki/Alpha_shape)
|
||||
|
||||
|
||||
|
||||
|
||||
[source code](src/jvmDemo/kotlin/alphashape/DemoAlphaShape.kt)
|
||||
[source code](src/jvmDemo/kotlin/alphashape/DemoAlphaShape01.kt)
|
||||
|
||||
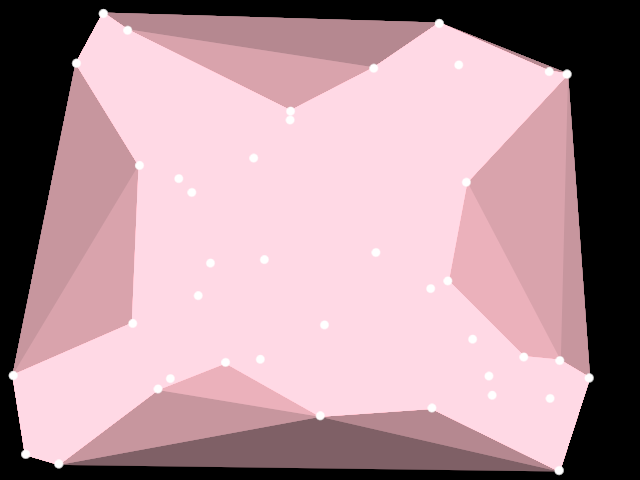
### alphashape/DemoAlphaShape02
|
||||
|
||||
Demonstrates the use of [AlphaShape] to create ten
|
||||
[org.openrndr.shape.ShapeContour] instances out of a collection of random [Vector2] points.
|
||||
|
||||
The same points are used for each contour, but an increased alpha parameter
|
||||
is passed to the AlphaShape algorithm. Higher values return more convex shapes
|
||||
= shapes with a larger surface.
|
||||
|
||||
The list of shapes is reversed to draw the smaller contours on top, otherwise only
|
||||
the last one would be visible.
|
||||
|
||||
An instance of [Random] with a fixed seed is used to ensure the resulting
|
||||
random shape is always the same.
|
||||
|
||||
|
||||
|
||||
[source code](src/jvmDemo/kotlin/alphashape/DemoAlphaShape02.kt)
|
||||
|
||||
### arrangement/DemoArrangement01
|
||||
|
||||
@@ -384,6 +406,14 @@ Demonstration of non-uniform contour blending
|
||||
|
||||
[source code](src/jvmDemo/kotlin/operators/DemoRoundCorners01.kt)
|
||||
|
||||
### operators/DemoRoundCorners02
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
[source code](src/jvmDemo/kotlin/operators/DemoRoundCorners02.kt)
|
||||
|
||||
### ordering/DemoHilbertOrder01
|
||||
|
||||
|
||||
|
||||
Reference in New Issue
Block a user